How Far Can You Go?

This morning I was ruminating about taking a math class.
And due to whatever reason I started thinking about maximal convex subsets.

What is it, actually?
It is a convex subset of a set that is maximal. That is, if you add any more points to this subset from the parent set, it becomes concave.

Now, it is trivial to say that if a convex set is its own maximal convex subset. And it is trivial to go one more step to say that a convex set has only one maximal convex subset (itself).

How about the converse of this "Theorem"?
If a set has only one maximal convex subset, is the set necessarily convex? Intuitively, the answer seems yes. But how do you prove it?

Now consider a non-convex set. How many maximal convex subsets does it have?

Consider the L-shaped set below:

 
It is easy to see that it has two maximal convex subsets:

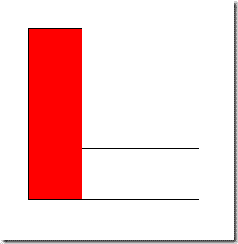
But is that all?

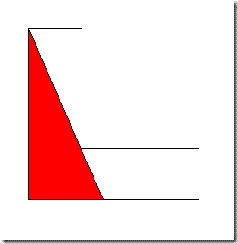
Probably not! What about this one?

 

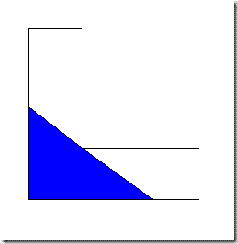
Or even this one?

It seems that there are an infinite number of maximal convex subsets for this L-shaped set.

In fact, any straight line passing through the corner of the L defines a maximal convex subset - the first two were just special cases of this.